Multivariate Kryptografie
Die multivariate Kryptografie wurde erstmals 1988 von Tsutomu Matsumoto
und Hideki Imai, zwei japanischen Kryptografen, vorgestellt. Sie umfasst
kryptografische Verfahren, die auf multivariaten Polynomen über
endlichen Körpern basieren. Ihr Fundament liegt in der vermuteten
Schwierigkeit des sogenannten MQ-Problems, bei dem ein multivariates
nichtlineares Gleichungssystem über einem endlichen Körper gelöst werden
soll. Dieses Problem ist NP-schwer, und bislang sind weder klassische
noch Quanten-Algorithmen bekannt, die es effizient lösen könnten. Aus
diesem Grund gelten Verfahren, die darauf aufbauen, als
vielversprechende Kandidaten für die Post-Quanten-Kryptografie. Die
Hauptanwendungsgebiete der multivariaten Kryptografie sind digitale
Signaturen und asymmetrische Verschlüsselungen. Diese Verfahren zeichnen
sich besonders durch ihre kurzen Signaturen von etwa \(0.5\) bis \(1.5\)
Kilobits aus.
Multivariate nicht-lineare Gleichungssysteme
Ein multivariates nichtlineares Gleichungssystem besteht aus \(m\)
Gleichungen \(f_1 = 0, \ldots, f_m = 0\), wobei \(f_i\) ein Polynom
\(d\)-ten Grades mit \(n\) verschiedenen Variablen über einem Körper
\(K\) ist.
Ein Beispiel für ein Gleichungssystem mit den Parametern \(m = 4\), \(d
= 2\), \(n = 4\) und \(K = \mathbb{Z}_2 = GF(2)\) ist:
\[ \begin{align*} x_0x_3 + x_2x_3 + x_0 + 1 = 0 \\ x_0x_1 + x_2x_3 + x_2
+ 1 = 0 \\ x_0x_1 + x_0x_3 + x_0 + x_1 + 1 = 0 \\ x_1x_2 + x_2x_3 + x_3
= 0 \\ \end{align*} \]
Eine Lösung dieses Gleichungssystems, \(x_0 = 1, x_1 = 0, x_2 = 1, x_3 =
0\), lässt sich durch einfaches Einsetzen überprüfen.
Es ist wichtig zu beachten, dass \(d > 1\) gelten muss, da andernfalls
das Gleichungssystem linear und somit leicht lösbar ist. Üblicherweise
wird mit quadratischen Gleichungen (also \(d = 2\)) gearbeitet.
Moderne Verfahren wie das sogenannte Rainbow Signature Scheme nutzen
beispielsweise \(K = GF(16)\) oder \(K = GF(256)\) mit etwa \(30\) bis
\(60\) Gleichungen und \(80\) bis \(200\) Variablen (s.
3.4.).
Aufbau und Falltüren
Die Struktur eines multivariaten Kryptografie-Verfahrens mit \(d=2\) zur
Erstellung digitaler Signaturen unter Verwendung des öffentlichen
Schlüssels \(P\) sowie der privaten Schlüssel \(S\), \(P'\) und \(T\)
ist wie folgt aufgebaut:

Abbildung 1: Aufbau eines multivariaten Kryptografie-Verfahrens zur
Erstellung digitaler Signaturen
Die privaten Schlüssel setzen sich folgendermaßen zusammen:
-
\(S: K^n \rightarrow K^n\) ist eine invertierbare affine Abbildung:\(S(\vec{x}) = D\vec{x} + \vec{e}\) mit \(D \in K^{n \times n}\) und \(\vec{x}, \vec{e} \in K^n\)
-
\(P': K^n \rightarrow K^m\) ist eine quadratische Abbildung, die das multivariate quadratische Polynomsystem mit \(n\) Variablen und \(m\) Gleichungen über dem endlichen Körper \(K\) repräsentiert. Dieses Polynomsystem ist so konstruiert, dass es effizient lösbar ist, da bei der Erstellung eine sogenannte Falltür integriert wurde - eine Methode, um dieses Gleichungssystem effizient zu lösen. Eine Erläuterung dazu folgt.
-
\(T: K^m \rightarrow K^m\) stellt ebenfalls eine invertierbare affine Abbildung dar. Sie folgt der Formel:\(T(\vec{x}) = F\vec{x} + \vec{g}\) mit \(F \in K^{m \times m}\) und \(\vec{x}, \vec{g} \in K^m\)
Der öffentliche Schlüssel \(P: K^n \rightarrow K^m\) entsteht durch die
Komposition bzw. Verkettung der genannten Abbildungen, \(P = T \circ P'
\circ S\). Hierbei handelt es sich bei \(P\) ebenfalls um ein
multivariates quadratisches Polynomsystem mit denselben Parametern wie
bei \(P'\). Allerdings wurden durch die affinen Abbildungen \(S\) und
\(T\) die ursprünglichen Polynome aus \(P'\) verborgen. Das soll dazu
führen, dass die in \(P'\) eingebaute Falltür nicht mehr nutzbar und
\(P\) daher nicht mehr effizient lösbar ist.
Um eine digitale Signatur zu erstellen, müssen die Gleichungssysteme
\(T, P'\) und \(S\) in der genannten Reihenfolge invertiert werden. Für
ein Dokument \(\vec{y} \in K^m\) kann dann die Signatur \(\vec{x} \in
K^n\) wie folgt erstellt werden:
\(\vec{y'} = T^{-1}(\vec{y})\)
\(\vec{x'} = P'^{-1}(\vec{y'})\)
\(\vec{x} = S^{-1}(\vec{x'})\)
Für die Verifikation wird dann mithilfe des öffentlichen Schlüssels
folgendes gebildet:
\(\vec{y} = P(\vec{x})\)
Zur asymmetrischen Verschlüsselung betrachten wir \(\vec{x} \in K^n\)
als Klartext und \(\vec{y} \in K^m\) als Geheimtext:
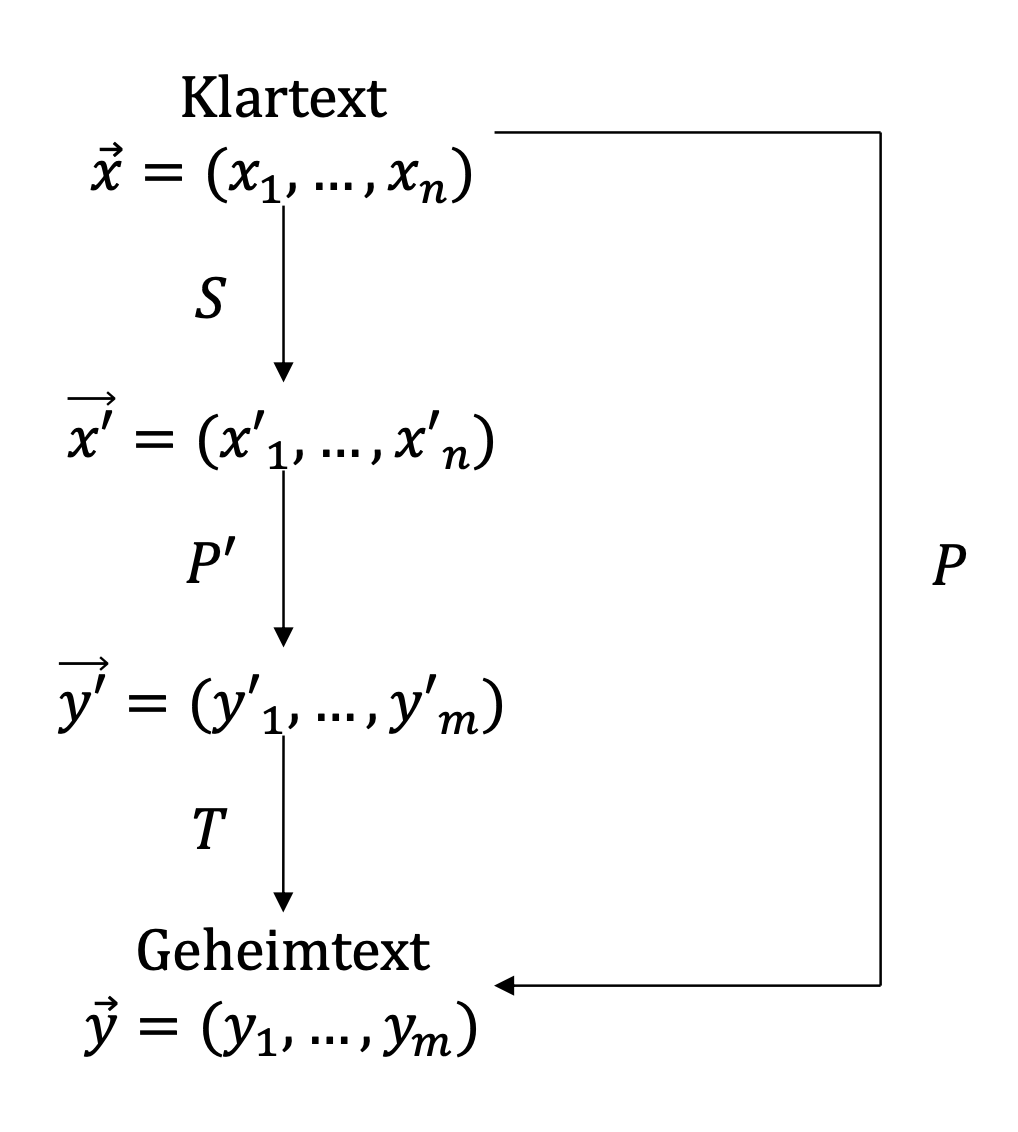
Abbildung 2: Aufbau eines multivariaten Kryptografie-Verfahrens zur
asymmetrischen Verschlüsselung
Zur Verschlüsselung eines Klartextes greift der Sender auf den
öffentlichen Schlüssel \(P\) des Empfängers zu und erstellt den
Geheimtext \(\vec{y} = P(\vec{x})\). Der Empfänger kann diesen
entschlüsseln, indem er ähnlich wie bei der Erstellung einer Signatur
schrittweise die privaten Abbildungen löst. In diesem Zusammenhang ist
von Bedeutung, dass \(P\) injektiv ist, da andernfalls keine eindeutige
Zuordnung zu einem Klartext möglich ist.
Wie bei der Konstruktion des privaten Polynomsystems \(P'\) eine Falltür
eingebaut wird und wie man diese nutzen kann, um \(P'\) effizient zu
lösen, hängt vom verwendeten Verfahren ab. Beispiele für grundlegende
Verfahren zur asymmetrischen Verschlüsselung sind das Step-wise
Triangular Sheme (STS), Matsumoto-Imai Scheme A (MIA) und Hidden Field
Equations (HFE) (s.
3.1.). Ein weiteres
Verfahren zur Erstellung digitaler Signaturen ist Unbalanced Oil and
Vinegar (UOV), das im nächsten Abschnitt genauer beschrieben wird.
Unbalanced Oil and Vinegar (UOV)
Das Oil and Vinegar Signatur-Schema wurde im Jahr 1997 von Jacques
Patarin vorgestellt. Der Name leitet sich von der Idee ab, Variablen in
zwei Kategorien aufzuteilen: Oil und Vinegar. Ähnlich der Zubereitung
eines Salatdressings sollen Öl und Essig, obwohl sie sich nicht mischen,
dennoch zusammenarbeiten, um etwas Neues und Nützliches zu schaffen.
Allerdings wurde das Schema bereits ein Jahr später gebrochen. Als
Reaktion darauf wurde 1999 das Unbalanced Oil and Vinegar Schema als
eine Verallgemeinerung des Originalschemas eingeführt. Hierbei werden
nicht gleichermaßen viele Oil- und Vinegar-Variablen genutzt, sondern
vermehrt Vinegar-Variablen eingesetzt. Dieses Verfahren gilt mit
geeigneten Parametern weiterhin als sicher.
Um dieses Signatur-Schema anzuwenden, müssen im ersten Schritt die
Anzahl an Oil-Variablen \(o\) und die Anzahl an Vinegar-Variablen \(v\)
festgelegt werden. Es wird empfohlen, diese so zu wählen, dass gilt \(v
\geq 2o\). Die Anzahl der Oil-Variablen entspricht der Anzahl der
Gleichungen der quadratischen Polynomsysteme, also ist \(m = o\). Die
Gesamtanzahl der Variablen entspricht der Summe der Oil- und
Vinegar-Variablen, also \(n = o + v\). Die invertierbare affine
Abbildung \(S: K^n \rightarrow K^n\) kann zufällig generiert werden. Auf
eine weitere affine Abbildung \(T\) wird bei diesem Verfahren
verzichtet, da diese weggelassen werden kann, ohne dabei die Sicherheit
zu beeinträchtigen. Da es mehr Variablen als Gleichungen gibt, ist
dieses Verfahren nicht injektiv und daher ausschließlich für die
Erzeugung digitaler Signaturen geeignet.
Die \(m\) Gleichungen des privaten Polynomsystems mit den Koeffizienten
\(a_{i,j,k}, b_{i,j,k}, c_{i,j}, d_{i,j}\) und \(e_i \in K\), den
Oil-Variablen \(O_1,...,O_{o} \in K\) und den Vinegar-Variablen
\(V_1,...,V_v \in K\) haben folgende Form:
\(y_i:= \sum\limits_{j=1}^{o}\sum\limits_{k=1}^{v}a_{i,j,k}O_jV_k\ +
\sum\limits_{j=1}^{v}\sum\limits_{k=1}^{v}b_{i,j,k}V_jV_k\ +
\sum\limits_{j=1}^{o}c_{i,j}O_j + \sum\limits_{j=1}^{v}d_{i,j}V_j +
e_i\) für \(1 \leq i \leq n\)
Anders gesagt: Die Gleichungen des Polynomsystems können zufällig
generiert werden, solange dabei darauf geachtet wird, dass kein Summand
vorkommt, der mehr als eine Oil-Variable als Faktor enthält. Dadurch
wird aus diesen quadratischen Polynomen ein lineares Gleichungssystem,
wenn man alle Vinegar-Variablen substituiert. Dies ist beim öffentlichen
Schlüssel \(P\) nicht möglich, da durch die Verkettung mit \(S\) im
öffentlichen Polynomsystem auch nach der Substitution quadratische
Summanden vorkommen können.
Um eine Signatur zu erstellen, muss nun eine Lösung für \(P'(\vec{x'}) =
\vec{y}\) gefunden werden. Hierfür wird ein zufälliger Vektor
\(\vec{x'_v} \in K^v\) gebildet und alle Vinegar-Variablen in \(P'\)
durch die Komponenten dieses Vektors substituiert. Dies führt zu einem
linearen Gleichungssystem \(Q'(\vec{x'_o})=\vec{y}\) mit \(o\)
Gleichungen und \(o\) Variablen. Es ist möglich, dass dieses
Gleichungssystem nicht lösbar ist. In diesem Fall muss ein anderer
zufälliger Vektor \(\vec{x'_v}\) gewählt werden. Nach der Lösung des
Gleichungssystems erhält man einen Lösungsvektor \(\vec{x'_o} \in K^o\).
Durch aneinanderhängen kann der Lösungsvektor \(\vec{x'} =
\begin{pmatrix} \vec{x'_o} \\ \vec{x'_v}\end{pmatrix}\) gebildet werden.
Abschließend muss lediglich \(S(\vec{x}) = \vec{x'}\) gelöst werden, um
eine Signatur \(\vec{x}\) zu erhalten. Diese kann anschließend mittels
\(P(\vec{x}) = \vec{y}\) verifiziert werden.
UOV Beispiel
Man wählt \(o = 2\), \(v = 4\) und \(K = \mathbb{Z}_2\). Somit gilt \(m
= o = 2\) und \(n = o + v = 6\).
Damit sind die Oil-Variablen \(x_0\) und \(x_1\) und die
Vinegar-Variablen \(x_2\) bis \(x_5\).
Man generiert eine zufällige affine Abbildung \(S\) und das private
Polynomsystem \(P'\):
Affine Abbildung: \(S(\vec{x}) = \begin{pmatrix} x_2 + x_4 +
x_5 + 1 \\ x_0 + x_3 + 1 \\ x_1 \\ x_0 +
x_1 \\ x_0 + x_2 + x_3 + x_5 + 1 \\ x_0 +
x_2 + x_3 + 1 \end{pmatrix}\)
Private Polynome: \(P'(\vec{x}) = \begin{pmatrix} x_0x_2 +
x_0x_5 + x_0 + x_1x_2 + x_1x_5 + x_1 +
x_2x_3 + x_2 + x_3x_4 + x_3 + x_4^2 +
x_4x_5 + x_5^2 + x_5 \\ x_0x_3 + x_0 +
x_1x_2 + x_1x_4 + x_2^2 + x_2x_4 +
x_2x_5 + x_2 + x_3x_4 + x_3x_5 + x_3 +
x_4^2 + x_4x_5 + x_5^2 + x_5 \end{pmatrix}\)
Anschließend kann der öffentliche Schlüssel berechnet werden:
Öffentliche Polynome: \(P(\vec{x}) = P' \circ S(\vec{x}) =
\begin{pmatrix} x_0^2 + x_0x_1 + x_0x_2 +
x_0x_3 + x_0x_4 + x_0x_5 + x_0 +
x_1^2 + x_1x_4 + x_1 + x_2x_4 + x_2 +
x_3x_4 + x_3 + x_5^2 + x_5 \\ x_0x_1 +
x_0x_4 + x_0 + x_1^2 + x_1x_2 +
x_1x_3 + x_1x_4 + x_1x_5 + x_2^2 +
x_2x_3 + x_2x_5 + x_2 + x_3 + x_4 +
x_5^2 + x_5 \end{pmatrix}\)
Nun soll eine Signatur zu \(\vec{y} = \begin{pmatrix} 1 \\ 0
\end{pmatrix}\) gefunden werden. Dazu wählt man zufällige Werte für alle
Vinegar-Variablen \(\vec{x'_v} = \begin{pmatrix} x'_2 \\ x'_3 \\
x'_4 \\ x'_5 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\
1 \\ 1 \end{pmatrix}\) und setzt diese in \(P'\) ein. Dadurch
erhält man: \(Q'(\vec{x'_o}) = \begin{pmatrix} x'_0 + x'_1 +
1 \\ x'_0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0
\end{pmatrix}\)
Durch Lösen des Gleichungssystems \(Q'(\vec{x'_o}) = \vec{y}\) erhält
man den Lösungsvektor \(\vec{x'_o} = \begin{pmatrix} x'_0 \\ x'_1
\end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}\) und damit
\(\vec{x'} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \\ 1
\\ 1 \end{pmatrix}\)
Zuletzt löst man das lineare Gleichungssystem \(S(\vec{x}) = \vec{x'}\)
und erhält die Signatur \(\vec{x} =\begin{pmatrix} 1 \\ 1 \\
1 \\ 0 \\ 0 \\ 0 \end{pmatrix}\).
Zur Verifikation bildet man nun: \(P(\vec{x}) = \begin{pmatrix} 1 \\
0 \end{pmatrix} = \vec{y}\)
UOV Rechner
Hier finden Sie den verwendeten Code zur Implementierung von UOV