Hashbasierte Kryptografie
Die hashbasierte Kryptografie wurde im Jahr 1979 mit der Einführung des
Lamport-Einmal-Signaturverfahrens von Leslie Lamport, einem
US-amerikanischen Mathematiker und Informatiker, ins Leben gerufen. Die
hashbasierte Kryptografie erlaubt die Umsetzung von Signaturverfahren,
deren Sicherheit auf der Unumkehrbarkeit und Kollisionsresistenz einer
zugrunde liegenden kryptografischen Hashfunktion basiert.
Dementsprechend ist, aufgrund der Unumkehrbarkeit, das einzige
Anwendungsgebiet die Erstellung von digitalen Signaturen. Bisher wurden
für diese Signaturverfahren keine Angriffe gefunden, die nicht durch
eine einfache Erhöhung der Sicherheitsparameter abgewehrt werden könnten
- selbst nicht mithilfe von Quantencomputern. Das macht sie zu
vielversprechenden Kandidaten für die Post-Quanten-Kryptografie. Die
grundlegenden Einmalsignaturverfahren zeichnen sich, neben ihrer
Sicherheit, besonders durch ihren geringen Rechenaufwand aus, allerdings
können sie, wie der Name schon sagt, nur einmal verwendet werden.
Alternativ ermöglichen modifizierte Verfahren Mehrfachsignaturen,
verlangen jedoch zusätzlichen Rechenaufwand.
Hashfunktionen
Eine Hashfunktion ist eine effizient berechenbare Abbildung, die eine
beliebig große Eingabemenge auf eine Zielmenge mit fester Größe
reduziert.
Beispielsweise könnte es eine Abbildung \(h\) geben, die als Eingabe
eine beliebig lange Zeichenfolge aus Nullen und Einsen entgegennimmt und
diese auf eine 16 Zeichen lange Zeichenfolge aus Nullen und Einsen
abbildet. Es könnte dann gelten:
\(h(0101) = 1110101011101000\)
\(h(1110000001010111) = 1111110000110101\)
\(h(101010101111100101000101010101010101110101) = 0000101011101110\)
Um Hashfunktionen in der Kryptografie nutzen zu können, müssen diese
bestimmte Anforderungen erfüllen. Hierzu gehören:
- Kollisionsresistenz
Hashfunktionen bilden eine größere Menge auf eine kleinere ab, wodurch
es unmöglich ist, Kollisionen zu vermeiden. Das bedeutet, es existieren
unterschiedliche Eingaben, die auf denselben Zielwert abgebildet werden
können.
Eine Hashfunktion \(h\) wird als stark kollisionsresistent
bezeichnet, wenn es für einen Angreifer unmöglich ist, in vertretbarer
Zeit zwei Eingabewerte \(x\) und \(x'\) zu finden, sodass gilt \(h(x) =
h(x')\).
"Unmöglich in vertretbarer Zeit" bedeutet, dass der erforderliche
Rechenaufwand so enorm ist, dass selbst moderne Hardware zu lange
braucht, um praktikabel zu sein.
Eine Hashfunktion \(h\) wird als schwach kollisionsresistent
bezeichnet, wenn es für einen Angreifer unmöglich ist, in vertretbarer
Zeit einen Eingabewert \(x' \neq x\) zu einem gegebenen \(x\) zu finden,
sodass gilt \(h(x') = h(x)\).
- Unumkehrbarkeit und Einwegfunktionen
Eine Hashfunktion \(h\) wird als unumkehrbar oder
Einwegfunktion
bezeichnet, wenn es für einen Angreifer unmöglich ist, in vertretbarer
Zeit zu einem gegebenen \(y\) ein \(x\) zu finden, sodass gilt \(h(x) =
y\).
- Kryptografische Hashfunktion
Eine Hashfunktion \(h\) wird als kryptografische Hashfunktion
bezeichnet, wenn sie sowohl stark kollisionsresistent als auch
unumkehrbar ist.
Die Familie der kryptografischen Hashfunktionen, bekannt als 'Secure
Hash Algorithm' (kurz SHA), beinhaltet verschiedene Varianten wie SHA-1,
SHA-2 und SHA-3. Es ist wichtig zu betonen, dass SHA-1 nicht mehr als
sicher gilt, während SHA-2 und SHA-3 als sicherere Alternativen
angesehen werden. Diese Hashfunktionen sind eine etablierte Gruppe
standardisierter Methoden zur Erzeugung von Hashwerten in der
Kryptografie.
Lamport-Einmal-Signaturverfahren
Das Lamport-Einmal-Signaturverfahren wurde erstmals 1979 von L. Lamport
vorgestellt. Es gilt mit angemessenen Sicherheitsparametern weiterhin
als robust gegenüber klassischen und Quanten-Algorithmen. Dennoch wird
es heutzutage in seiner ursprünglichen Form nicht mehr verwendet, da es
nur einmal genutzt werden kann und die resultierenden Signaturen sehr
lang sind. Trotzdem bildet es eine solide Grundlage, um eine tiefere
Auseinandersetzung mit der hashbasierten Kryptografie zu ermöglichen,
weshalb es hier vorgestellt wird.
Folgende Komponenten werden benötigt:
- Eine zu signierende Nachricht \(m \in \{0,1\}^*\)
- Einen Sicherheitsparameter \(n \in \mathbb{N}\)
- Eine kryptografische Hashfunktion \(f: \{0,1\}^* \rightarrow
\{0,1\}^n\)
- Eine Einwegfunktion \(g: \{0,1\}^n \rightarrow \{0,1\}^n\)
- Privater Schlüssel
Für den privaten Schlüssel \(X\) generiert man \(n\) Paare, jeweils
bestehend aus zwei zufälligen Zeichenfolgen aus Nullen und Einsen der
Länge \(n\):
Privater Schlüssel: \(X = \begin{pmatrix} x_{0,0} ; x_{0,1} \\ x_{1,0} ;
x_{1,1} \\ ... \\ x_{n-1,0} ; x_{n-1,1} \end{pmatrix}\) mit \(x_{i,j}
\in \{0,1\}^n\)
- Öffentlicher Schlüssel
Für den öffentlichen Schlüssel \(Y\) bildet man erneut \(n\) Paare aus
jeweils zwei Zeichenfolgen aus Nullen und Einsen der Länge \(n\), indem
man auf alle Werte im privaten Schlüssel die Einwegfunktion \(g\)
anwendet:
Öffentlicher Schlüssel: \(Y = \begin{pmatrix} g(x_{0,0}) ; g(x_{0,1}) \\
g(x_{1,0}) ; g(x_{1,1}) \\ ... \\ g(x_{n-1,0}) ; g(x_{n-1,1})
\end{pmatrix} = \begin{pmatrix} y_{0,0} ; y_{0,1} \\ y_{1,0} ; y_{1,1}
\\ ... \\ y_{n-1,0} ; y_{n-1,1} \end{pmatrix}\) mit \(y_{i,j} \in
\{0,1\}^n\)
Erstellen der Signatur
Zuerst wird mithilfe der Nachricht \(m\) und der kryptografischen
Hashfunktion \(f\) der Hashwert \(h = f(m) \in \{0,1\}^n\) gebildet.
Anschließend kann die Signatur \(S\) gebildet werden, indem aus jedem
Paar in \(X\) ein Wert gewählt wird. Ist das \(i\)-te Bit in \(h\)
gleich \(0\), gilt \(s_i = x_{i,0}\), handelt es sich um eine \(1\),
gilt \(s_i = x_{i,1}\).
Signatur: \(S = \begin{pmatrix} x_{0,h[0]} \\ x_{1,h[1]} \\ ... \\
x_{n-1,h[n-1]} \end{pmatrix} = \begin{pmatrix} s_0 \\ s_1 \\ ... \\
s_{n-1} \end{pmatrix}\) mit \(s_i \in \{0,1\}^n\)
Mit \(h[i]\) ist hier das Bit mit dem Index \(i\) in der Zeichenfolge
\(h\) gemeint.
Verifikation der Signatur
Zuerst bildet der Empfänger ebenfalls \(h = f(m) \in \{0,1\}^n\).
Anschließend muss die Einwegfunktion \(g\) auf alle Komponenten der
Signatur \(S\) angewendet werden, um \(V\) zu bilden:
Hashwerte der Signatur: \(V = \begin{pmatrix} g(s_0) \\ g(s_1) \\ ... \\
g(s_{n-1}) \end{pmatrix} = \begin{pmatrix} v_0 \\ v_1 \\ ... \\ v_{n-1}
\end{pmatrix}\) mit \(v_i \in \{0,1\}^n\)
Um die Signatur zu verifizieren, müssen die Komponenten in \(V\) ähnlich
wie bei der Erstellung der Signatur mit den entsprechenden Komponenten
im öffentlichen Schlüssel \(Y\) verglichen werden. Ist das \(i\)-te Bit
in \(h\) gleich \(0\), muss gelten \(v_i = y_{i,0}\), handelt es sich um
eine \(1\), muss gelten \(v_i = y_{i,1}\).
Es muss also gelten : \(\begin{pmatrix} v_0 \\ v_1 \\ ... \\ v_{n-1}
\end{pmatrix} = \begin{pmatrix} y_{0,h[0]} \\ y_{1,h[1]} \\ ... \\
y_{n-1,h[n-1]} \end{pmatrix}\)
Lamport-Einmal-Signaturverfahren Beispiel
Zur Verbesserung der Übersichtlichkeit verwenden wir in diesem Beispiel
den Sicherheitsparameter \(n = 8\). Die Zeichenfolgen aus Nullen und
Einsen stellen wir in Dezimaldarstellung dar, also als ganze Zahl von
\(0\) bis \(2^n-1 = 255\). Sowohl als kryptografische Hashfunktion
\(f\), als auch als Einwegfunktion \(g\) nutzen wir die Hashfunktion
"SHA256", eine Variante des kryptografischen Hashalgorithmus "Secure
Hash Algorithm", dem der Bitstring als Eingabe übergeben wird. In diesem
Fall werden aber lediglich die ersten 8-Bits der Ausgabe als Hashwerte
verwendet.
Privater Schlüssel
Erst generiert man \(8\) Paare man aus jeweils zwei Werten aus
\(\{0,...,255\}\), um den privaten Schlüssel zu erhalten:
Privater Schlüssel: \(X = \begin{pmatrix}185 ; 77 \\ 143 ; 4 \\ 214 ; 5
\\ 99 ; 178 \\ 6 ; 134 \\ 217 ; 53 \\ 10 ; 244 \\ 43 ; 72\end{pmatrix}\)
Öffentlicher Schlüssel
Anschließend kann der öffentliche Schlüssel gebildet werden, indem \(8\)
Paare aus den Hashwerten der entsprechenden Werte im privaten Schlüssel
mithilfe der Einwegfunktion \(g\) gebildet werden:
Öffentlicher Schlüssel: \(Y = \begin{pmatrix}g(185) ; g(77) \\ g(143) ;
g(4) \\ g(214) ; g(5) \\ g(99) ; g(178) \\ g(6) ; g(134) \\ g(217) ;
g(53) \\ g(10) ; g(244) \\ g(43) ; g(72)\end{pmatrix} =
\begin{pmatrix}97 ; 168 \\ 214 ; 75 \\ 128 ; 239 \\ 140 ; 1 \\ 231 ; 93
\\ 22 ; 40 \\ 74 ; 130 \\ 68 ; 135\end{pmatrix}\)
Erstellen der Signatur
Mithilfe des vorliegenden privaten Schlüssels kann nun eine beliebige
Nachricht signiert werden. Zur Signatur der Nachricht \(m =\) "Hallo
Welt!" muss als erstes der Hashwert mithilfe der kryptografischen
Hashfunktion \(f\) gebildet werden. Dies ist möglich, da sich jede
Zeichenfolge, einschließlich "Hallo Welt!", entsprechend einer Kodierung
für Unicode-Zeichen (hier UTF-8), in Binärdarstellung, also als Wert aus
\(\{0,1\}^*\), darstellen lässt:
Hashwert der Nachricht in Binärdarstellung:
\(h = f(m) \) \(= f(01001000 01100001 01101100 01101100 01101111 00100000 01010111 01100101 01101100 01110100 00100001_2) \) \(= 10100101_2\)
\(h = f(m) \) \(= f(01001000 01100001 01101100 01101100 01101111 00100000 01010111 01100101 01101100 01110100 00100001_2) \) \(= 10100101_2\)
Entsprechend dieser Zeichenfolge aus Nullen und Einsen \(h\) kann nun
die Signatur aus dem privaten Schlüssel \(X\) zusammengestellt werden.
Da das erste Zeichen in \(h\) eine \(1\) ist, wählt man aus der ersten
Zeile in \(X\) den zweiten Wert. Da das zweite Zeichen in \(h\) eine
\(0\) ist, wählt man aus der zweiten Zeile in \(X\) den ersten Wert, und
so weiter.
Signatur: \(S = \begin{pmatrix}77 \\ 143 \\ 5 \\ 99 \\ 6 \\ 53 \\ 10 \\
72\end{pmatrix}\)
Verifikation der Signatur
Dem Empfänger liegen nun die Nachricht \(m\), die Signatur \(S\) und der
öffentliche Schlüssel \(Y\) vor. Darüber hinaus kennt er die
kryptografische Hashfunktion \(f\) und die Einwegfunktion \(g\).
Um die Signatur zu verifizieren, bildet der Empfänger nun ebenfalls den
Hashwert \(h\) der Nachricht mithilfe der kryptografischen Hashfunktion
\(f\). Darüber hinaus werden die Hashwerte aller Komponenten der
Signatur \(S\) mithilfe der Einwegfunktion \(g\) gebildet und als \(V\)
zusammengefasst:
Hashwert der Nachricht in Binärdarstellung: \(h = f(m) = 10100101_2\)
Hashwerte der Signatur: \(V = \begin{pmatrix}g(77) \\ g(143) \\ g(5) \\
g(99) \\ g(6) \\ g(53) \\ g(10) \\ g(72)\end{pmatrix} =
\begin{pmatrix}168 \\ 214 \\ 239 \\ 140 \\ 231 \\ 40 \\ 74 \\
135\end{pmatrix}\)
Zuletzt muss der Empfänger die Komponenten von \(V\) mit denen aus \(Y\)
vergleichen. Da das erste Zeichen in \(h\) eine \(1\) ist, muss der Wert
in der ersten Zeile in \(V\) dem zweiten Wert in der ersten Zeile in
\(Y\) entsprechen. Da das zweite Zeichen in \(h\) eine \(0\) ist, muss
der Wert in der zweiten Zeile in \(V\) dem ersten Wert in der zweiten
Zeile in \(Y\) entsprechen, und so weiter.
Die Signatur ist gültig, da hier gilt: \(\begin{pmatrix} v_0 \\ v_1 \\
... \\ v_{7} \end{pmatrix} = \begin{pmatrix} 168 \\ 214 \\ ... \\ 135
\end{pmatrix} = \begin{pmatrix} y_{0,1} \\ y_{1,0} \\ ... \\ y_{7,1}
\end{pmatrix}\)
Mehrfachsignaturen
Da bei jeder Signatur die Hälfte des privaten Schlüssels veröffentlicht
werden muss, lässt sich, wie der Name bereits impliziert, das
Lamport-Einmal-Signaturverfahren nur einmal pro Schlüsselpaar verwenden.
Dasselbe gilt für das sogenannte "Winternitz Einmalsignaturverfahren",
ein weiteres grundlegendes Verfahren der hashbasierten Kryptografie (s.
4.1.). Es sind zwei
Methoden bekannt, die es ermöglichen, diese Einmalsignaturverfahren zu
Mehrfachsignaturverfahren zu modifizieren: Das Chaining von Nachrichten
und das Merkle-Baum Signaturverfahren.
Chaining
Beim Chaining veröffentlicht der Sender am Ende jeder signierten
Nachricht einen neuen öffentlichen Schlüssel, mit dem die jeweils
folgende Nachricht verifiziert werden kann.
Dadurch ist es zum Verifizieren der Signatur einer Nachricht jedoch
notwendig, dass dem Empfänger ebenfalls alle vorherigen Signaturen
vorliegen. Diese müssen bei jeder Nachricht angehängt werden. Das
bedeutet, dass die Länge der Signatur einer Nachricht mit jeder weiteren
Iteration des Verfahrens linear ansteigt. Darüber hinaus steigt auch der
Rechenaufwand, den der Empfänger beim Verifizieren leisten muss, da er
jede einzelne Nachricht der Kette prüfen muss. Außerdem wird mit jeder
Signatur zusätzliche Information veröffentlicht, nämlich wie viele
Signaturen bereits erstellt wurden. Aus diesen Gründen wird auf dieses
Verfahren in der Regel zugunsten des Merkle-Baum Signaturverfahrens
verzichtet.
Merkle-Baum Signaturverfahren
Das Merkle-Baum Signaturverfahren bietet eine Alternative zum Chaining,
bei der der Aufwand lediglich logarithmisch mit der Anzahl der
Signaturen steigt, indem ein Binärbaum anstelle einer Kette genutzt
wird. Allerdings muss zu Beginn die Anzahl der maximal möglichen
Signaturen festgelegt werden, was je nach Anwendungsfall Vor- und
Nachteile haben kann. Im Vergleich zu RSA ist dieses Verfahren zwar eher
ineffizient, jedoch stellt es eine vielversprechende Methode für
zukünftige digitale Signaturen dar, da es als sicher gegen Angriffe
mittels Quantencomputern gilt.
Als erstes muss eine Höhe \(H \in \mathbb{N} \geq 2\) des Binärbaumes
festgelegt werden. Jedes Blatt dieses Binärbaumes entspricht einer
möglichen Signatur. Bei einem Binärbaum der Höhe \(H\) sind also \(2^H\)
Signaturen möglich. Zusätzlich müssen ein Einmalsignaturverfahren und
eine kryptografische Hashfunktion \(f\) ausgewählt werden.
Jedem Blatt wird nun ein privater Schlüssel \(X_i\) und ein
entsprechender öffentlicher Schlüssel \(Y_i\), mit \(0 \leq i < 2^H\),
des gewählten Einmalsignaturverfahrens zugewiesen. Der Wert eines jeden
Blattes ist dann der Hashwert des entsprechenden öffentlichen
Schlüssels, den man mithilfe der kryptografischen Hashfunktion \(f\)
berechnet.
Die Knoten des Binärbaumes nennt man \(k_{j,i}\). Hier ist \(j\) die
Ebene im Binärbaum (also \(j = H\) bei den Blättern) und \(i\) deren
Index, wenn man beginnend bei \(0\) von links nach rechts zählt.
Für die Blätter gilt: \(k_{H,i} = f(Y_i\)).
Allen anderen Knoten im Binärbaum wird der Hashwert der
aneinandergehängten Werte seiner beiden Kindknoten zugewiesen: \(k_{j,i}
= f(k_{j+1,2i}||k_{j+1,2i+1})\).
Der Wert der Wurzel des Binärbaumes ist der übergeordnete öffentliche
Schlüssel des Verfahrens.
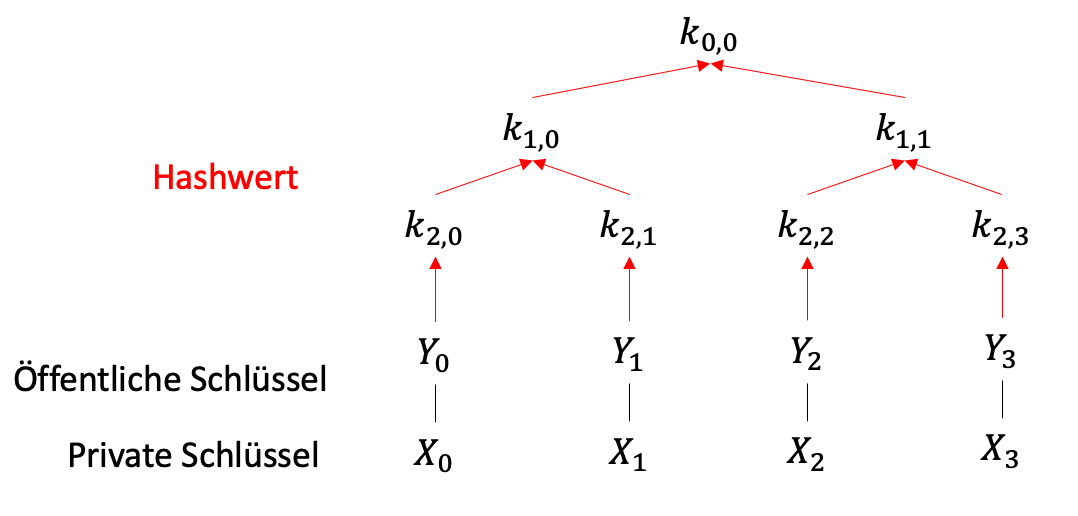
Abbildung 1: Merkle-Baum mit der Höhe \(H = 2\)
Um eine Nachricht zu signieren, wählt der Sender den nächsten
unbenutzten privaten Schlüssel und bildet die Signatur mithilfe des
Einmalsignaturverfahrens. Anschließend veröffentlicht er, wie immer, die
Nachricht, die Signatur und den passenden öffentlichen Schlüssel zum
genutzten privaten Schlüssel. Zusätzlich veröffentlicht er den Index des
genutzten Blattes und die Hashwerte der Geschwisterknoten aller Knoten,
die auf dem Pfad von dem genutzten Blatt zur Wurzel liegen.
Beispiel anhand Abbildung 1:
Wenn wir \(X_1\) verwendet haben, liegen \(k_{2,1}\) und \(k_{1,0}\) auf
dem Pfad zur Wurzel \(k_{0,0}\). Es müssen also die Werte der
Geschwisterknoten von \(k_{2,1}\) und \(k_{1,0}\), also \(k_{2,0}\) und
\(k_{1,1}\), mitveröffentlicht werden. Des Weiteren veröffentlichen wir
den Index des Blattes, also in diesem Fall \(i = 1\).
Um eine Signatur zu verifizieren, muss nun zuerst der mitgesendete
öffentliche Schlüssel verifiziert werden. Dazu wird der Hashwert von
diesem mittels der kryptografischen Hashfunktion \(f\) gebildet. Dieser
Hashwert wird nun mit dem ersten mitgesendeten Hashwert der
Geschwisterknoten konkateniert und von dem Ergebnis erneut der Hashwert
berechnet. Ist der mitgesendete Index dabei gerade, muss der
mitgesendete Hashwert hinten an den vorliegenden Hashwert angehängt
werden, ansonsten vorne. Anschließend wird der Index des Elternknotens
mit \(i_{Eltern} = \lfloor \frac {i_{Kind}}{2} \rfloor\) berechnet. Mit
dem neuen Hashwert wird der nächste mitgesendete Geschwisterknoten
konkateniert und gehasht, und so weiter. Erhält man am Ende einen Wert,
der mit dem des übergeordneten öffentlichen Schlüssels, also der Wurzel
des Binärbaumes, übereinstimmt, gilt der öffentliche Schlüssel als
gültig. Anschließend kann die Gültigkeit der Signatur entsprechend des
Einmalsignaturverfahrens mithilfe des verifizierten öffentlichen
Schlüssels geprüft werden.
Beispiel anhand Abbildung 1:
Der Empfänger bildet den Hashwert des mitgesendeten öffentlichen
Schlüssels \(Y_1\) und erhält \(k_{2,1}\). Da \(i=1\) ungerade ist, wird
der erste mitgesendete Hashwert \(k_{2,0}\) vorne an \(k_{2,1}\)
angehängt. Er bildet also den Hashwert \(f(k_{2,0}||k_{2,1})\) und
erhält \(k_{1,0}\). Den Index dieses Knotens berechnet er mittels
\(i_{Eltern} = \lfloor \frac {1}{2} \rfloor = 0\). Dann hängt er
\(k_{1,1}\) hinten an den neuen Hashwert, da der neue Index gerade ist.
Er bildet den Hashwert \(f(k_{1,0}||k_{1,1})\) und erhält \(k_{0,0}\).
Damit gilt \(Y_1\) gültig, da \(k_{0,0}\) der übergeordnete öffentliche
Schlüssel ist.
Der Mehraufwand setzt sich also daraus zusammen, dass bei jeder Signatur
\(H\) weitere Hashwerte und ein Index mitgesendet werden müssen und bei
jeder Verifikation \(H\) weitere Hashwerte gebildet werden müssen. Ein
weiterer nennenswerter Umstand ist, dass das Merkle-Baum
Signaturverfahren nicht zustandslos ist. Der Signierer muss also immer
den gesamten Binärbaum und die Information, welche Blätter bereits
genutzt wurden, speichern, um diesen weiter nutzen zu können.
Lamport-Einmal-Signaturverfahren Rechner
Hier finden Sie den verwendeten Code zur Implementierung des
Lamport-Einmal-Signaturverfahrens