Grundlagen

Auf dieser Seite werden einige Kryptografiebegriffe erläutert, die bekannt sein sollten, um die nachfolgenden Inhalte nachvollziehen zu können. Dazu zählen symmetrische und asymmetrische Verschlüsselung, digitale Signaturen und die entsprechenden Grundlagen, die mit diesen Konzepten zusammenhängen.

Es werden mathematische Grundlagen auf einem Niveau vorausgesetzt, die man in etwa nach einem Semester eines ingenieurs- bzw. naturwissenschaftlichen Studiengangs erworben haben sollte.

Dazu gehören grundlegende Kenntnisse der linearen Algebra, wie das Rechnen mit Matrizen und Vektoren sowie das Lösen linearer Gleichungssysteme. Begriffe wie die Inverse oder Determinante einer Matrix, affine Abbildungen und lineare (Un-)Abhängigkeit sollten ebenfalls bekannt sein. Darüber hinaus sollte man über die Grundlagen der modularen Arithmetik verfügen und das Rechnen in endlichen Körpern beherrschen (s. 1.1. - 1.2).

Symmetrische Verschlüsselung

Symmetrische Verschlüsselungsverfahren, auch als symmetrische Kryptosysteme bezeichnet (englisch: Secret-key cryptography), ermöglichen eine verschlüsselte Kommunikation, bei der jeder Kommunikationsteilnehmer denselben geheimen Schlüssel verwendet. Dieser Schlüssel ermöglicht es, sowohl Klartexte zu verschlüsseln als auch Geheimtexte zu entschlüsseln.

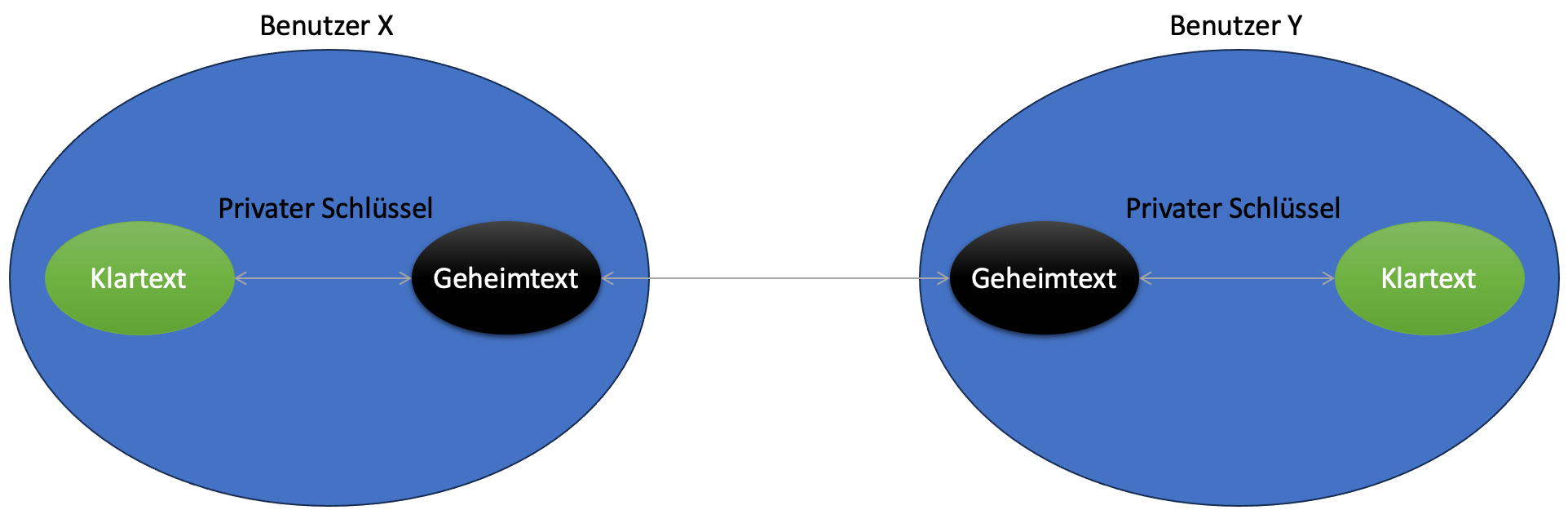
Abbildung 1: Visuelle Darstellung einer symmetrisch verschlüsselten Kommunikation

Diese Verschlüsselungsverfahren werden bereits seit der Antike verwendet. Ein bekanntes Beispiel ist die sogenannte Caesar-Chiffre. Bei dieser Methode dient eine ganze Zahl, beispielsweise \(4\), als privater Schlüssel. Für die Verschlüsselung wird dann jeder Buchstabe des Klartextes durch den vierten Buchstaben im Alphabet, der auf ihn folgt, ersetzt. Dabei wird nach dem Buchstaben Z wieder bei A begonnen. Auf diese Weise wird aus einem A ein E, aus einem B ein F und so weiter. Für die Entschlüsselung des Geheimtextes werden die Buchstaben durch ihre entsprechenden Vorgänger ersetzt.

Heutzutage kommt häufig das sogenannte Advanced Encryption Standard (AES)-Verfahren zum Einsatz. Dieses zeichnet sich durch hohe Sicherheit und Effizienz aus und gilt mit entsprechenden Sicherheitsparametern sogar als widerstandsfähig gegen Angriffe durch Quantencomputer.

Ein häufig auftretendes Problem im Zusammenhang mit symmetrischer Verschlüsselung ist die große Anzahl an notwendigen Schlüsseln in einem umfangreichen Netzwerk, in dem jeder mit jedem kommuniziert. Für \(n\) Teilnehmer werden \(\frac {n(n-1)}{2}\) Schlüssel benötigt. Der benötigte Speicherplatz steigt also quadratisch mit der Anzahl der Teilnehmer an.

Darüber hinaus besteht die Herausforderung des komplexen Schlüsselaustauschs: Die Kommunikationsteilnehmenden müssen im Voraus eine gemeinsame Vereinbarung über einen geheimen Schlüssel treffen. Diese Schlüsselaustauschphase muss vertraulich ablaufen. Da es mit ausschließlich symmetrischen Verschlüsselungsverfahren schwierig ist, dieses Problem zu bewältigen, wird dafür auf ein anderes Konzept zurückgegriffen.

Asymmetrische Verschlüsselung

Asymmetrische Verschlüsselungsverfahren, auch als asymmetrische Kryptosysteme bezeichnet (englisch: Public-key cryptography), ermöglichen eine verschlüsselte Kommunikation, bei der jeder Kommunikationsteilnehmer über ein Schlüsselpaar verfügt. Der öffentliche Schlüssel wird zur Verschlüsselung von Klartexten verwendet und jedem Teilnehmer des Netzwerkes zur Verfügung gestellt. Der private Schlüssel dient der Entschlüsselung von Geheimtexten und wird geheim gehalten.

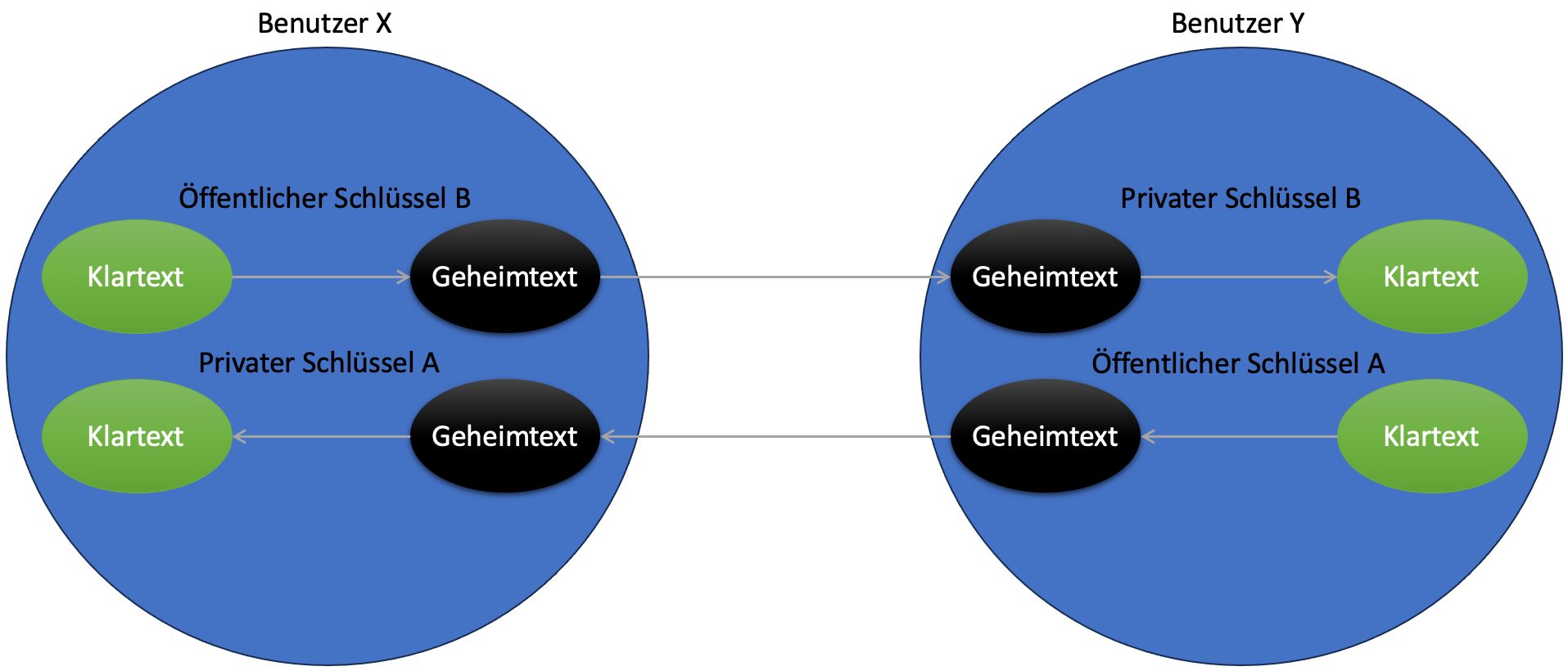
Abbildung 2: Visuelle Darstellung einer asymmetrisch verschlüsselten Kommunikation

Das Prinzip ist vergleichbar mit der Nutzung eines Briefkastens. Jeder hat die Möglichkeit, etwas in den Briefkasten zu werfen, aber nur der Besitzer des Briefkastens kann diesen öffnen und die darin befindlichen Briefe herausnehmen. In diesem Kontext entspricht das Einwerfen eines Briefs dem Verschlüsselungsvorgang unter Verwendung des öffentlichen Schlüssels des Empfängers. Das Herausnehmen der Briefe hingegen steht für den Entschlüsselungsvorgang mittels des privaten Schlüssels, der ausschließlich dem Empfänger zugänglich ist.

Ein prominentes Verfahren, das heutzutage weit verbreitet ist, stellt das Rivest-Shamir-Adleman-Verfahren (kurz: RSA) dar. Es beruht auf dem mathematischen Problem der Faktorisierung großer Zahlen und kann für die asymmetrische Verschlüsselung und die Erstellung digitaler Signaturen eingesetzt werden.

Da sich zur Kommunikation mittels asymmetrischer Verschlüsselung nicht vorher auf einen Schlüssel geeinigt werden muss, ist das Problem des schwierigen Schlüsselaustausches damit gelöst. Zudem wird lediglich ein Schlüsselpaar pro Kommunikationsteilnehmer benötigt. Selbst in einem großen Netzwerk mit \(n\) Teilnehmern, in dem jeder mit jedem kommunizieren können soll, sind lediglich \(2n\) Schlüssel erforderlich.

Dennoch birgt auch die asymmetrische Verschlüsselung einige Nachteile. Dazu gehört zum Beispiel ein erhöhter Rechenaufwand oder der Fakt, dass viele Verfahren dieser Art, unter anderem RSA, als nicht sicher gegen Angriffe durch Quantencomputer gelten. Ein häufig angewandter Ansatz zur Bewältigung dieser Herausforderungen besteht darin, hybride Verfahren einzusetzen. Dabei erfolgt der erste Schlüsselaustausch mittels eines quantensicheren asymmetrischen Verfahrens, gefolgt von der Nutzung eines symmetrischen Verfahrens für die eigentliche Kommunikation.

Ein zusätzliches Problem ergibt sich durch mangelnde Authentizität. Dies bedeutet, dass ein Kommunikationsteilnehmer, der etwas verschlüsseln möchte, nicht sicher sein kann, ob ein öffentlicher Schlüssel tatsächlich dem behaupteten Empfänger gehört. Ein Lösungsansatz für dieses Problem ist das Konzept der digitalen Signaturen.

Digitale Signaturen

Digitale Signaturverfahren haben die Aufgabe, herkömmliche Unterschriften für digitale Dokumente zu simulieren. Das bedeutet, dass jeder in der Lage sein soll, eine digitale Signatur zu verifizieren, während nur der Unterzeichner in der Lage ist, eine gültige Signatur für sich zu erstellen. Zusätzlich wird durch die digitale Signatur das unterzeichnete Dokument vor nachträglichen Veränderungen geschützt.

Für die Erstellung einer digitalen Signatur wird, ähnlich wie bei der asymmetrischen Verschlüsselung, ein Schlüsselpaar pro Kommunikationsteilnehmer benötigt. Der private Schlüssel bleibt geheim, während der öffentliche Schlüssel bei einer Zertifizierungsstelle hinterlegt wird, wo ihn jeder andere Kommunikationsteilnehmer einsehen kann. Der Unterzeichner nutzt seinen privaten Schlüssel, um eine Signatur für sein Dokument oder seine Nachricht zu erstellen. Anschließend werden sowohl die Signatur als auch das Dokument an den Empfänger übermittelt.

Der Empfänger erhält über die Zertifizierungsstelle den öffentlichen Schlüssel des Unterzeichners, um sicherzustellen, dass dieser Schlüssel tatsächlich dem Unterzeichner zugeordnet ist. Mithilfe dieses öffentlichen Schlüssels kann der Empfänger das Dokument bzw. die Nachricht aus der Signatur wiederherstellen. Wenn das wiederhergestellte Dokument mit dem mitgelieferten Dokument übereinstimmt, gilt die Signatur als gültig.

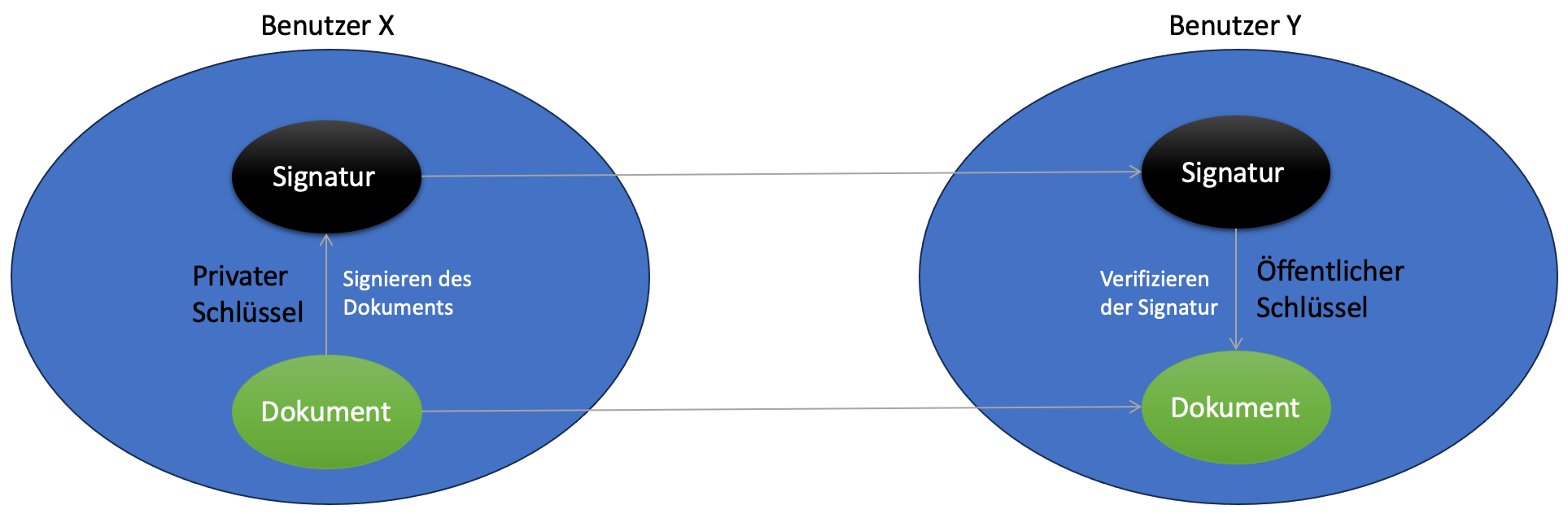
Abbildung 2: Visuelle Darstellung der Erstellung und Verifikation einer digitalen Signatur

Digitale Signaturverfahren lassen sich häufig aus asymmetrischen Verschlüsselungsverfahren ableiten. So wird beispielsweise RSA auch für die Erzeugung digitaler Signaturen verwendet. Es existieren jedoch auch Signaturverfahren, bei denen das nicht zutrifft. Ein Beispiel dafür ist das Elliptic Curve Digital Signature Algorithm (ECDSA) Verfahren, das auf den Sicherheitseigenschaften von elliptischen Kurven basiert.