Gitterbasierte Kryptografie
Die gitterbasierte Kryptografie (engl. lattice-based cryptography) wurde
erstmals 1996 von Miklós Ajtai, einem ungarischen Informatiker,
vorgestellt. Sie beschäftigt sich mit Verfahren, die auf der vermuteten
schweren Lösbarkeit gewisser Gitterprobleme beruhen. Diese Verfahren
zeichnen sich durch hohe Sicherheit, vergleichsweise effiziente
Implementierungen und große Simplizität aus. Zusätzlich wird angenommen,
dass sie gegenüber Quantencomputern sicher sind. Bisher ist weder ein
klassischer noch ein Quanten-Algorithmus bekannt, der in polynomieller
Laufzeit eine Lösung für eines der zugrundeliegenden Gitterprobleme
liefern kann. Gitterbasierte Kryptografie findet vor allem Anwendung in
asymmetrischen Verschlüsselungen und der Erzeugung digitaler Signaturen.
Gitter
In der Mathematik bezeichnet ein Gitter die Menge von Punkten in einem
\(n\)-dimensionalen Raum, die eine periodische Struktur aufweisen und
sich als ganzzahlige Linearkombination von \(m\) linear unabhängigen
Vektoren \(b_1,...,b_m \in \mathbb{R}^n\) darstellen lassen. Die
Vektoren \(b_1,...,b_m\) werden als Basis des Gitters bezeichnet und in
der Regel als Matrix \(B \in \mathbb{R}^{n\times m}\) mit den
Spaltenvektoren \(b_1,...,b_m\) zusammengefasst. Das Gitter, welches
durch diese Basis generiert wird, ist die Menge der Vektoren
\(\mathcal{L}(B)=\{Bx | x \in \mathbb{Z}^m\}\).
In anderen Worten: Im \(n\)-dimensionalen Raum liegt ein Satz aus \(m\)
Vektoren vor, die in verschiedene Richtungen zeigen. Jeder Punkt, den
man erreichen kann, indem man diese Vektoren in ihrer ursprünglichen
oder in entgegengesetzter Richtung beliebig oft aneinanderreiht, gehört
zu dem Gitter.
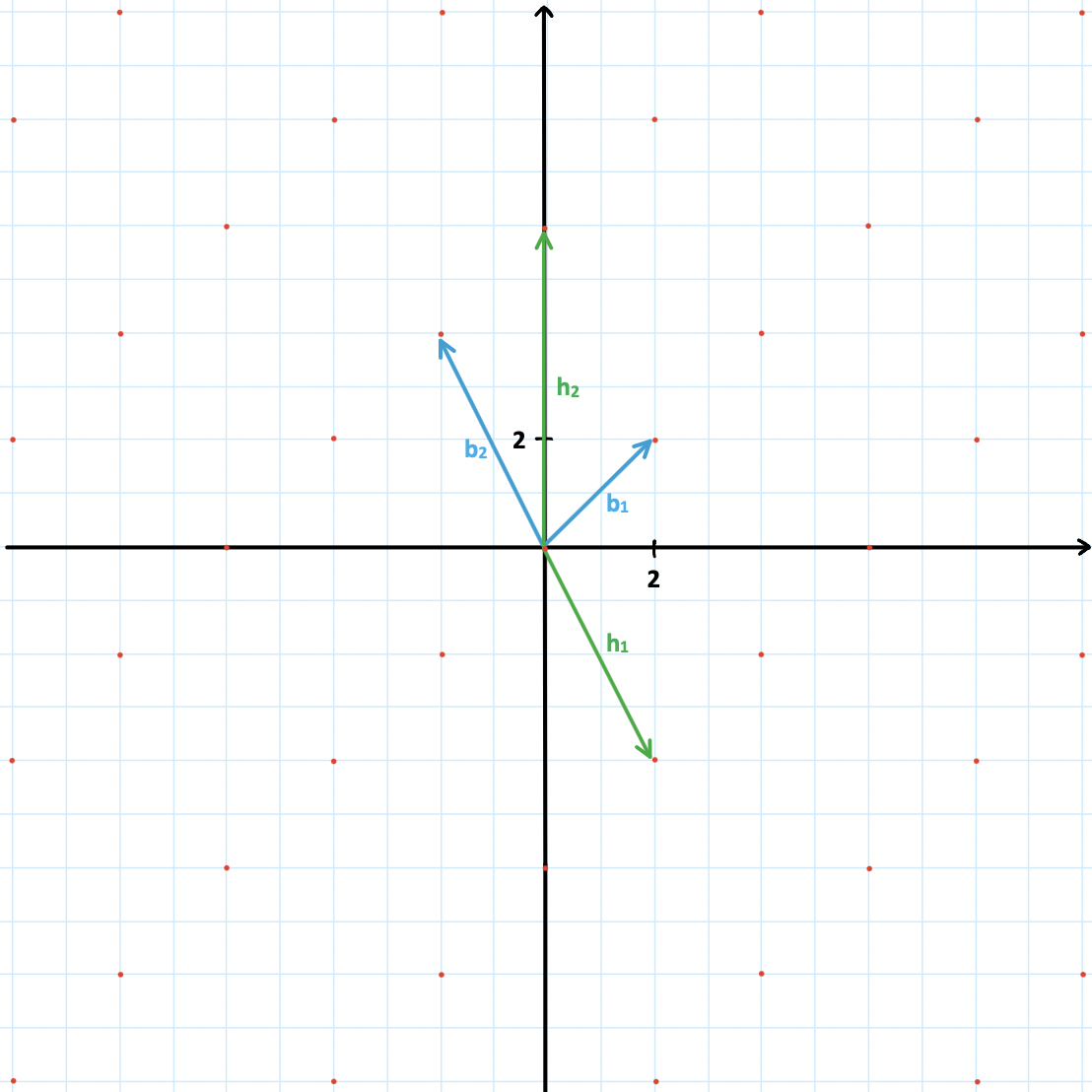
Abbildung 1: 2-dimensionales Gitter mit den Basen \(B=\{b_1,b_2\}\)
und \(H=\{h_1,h_2\}\)
In Abbildung 1 ist ein Ausschnitt des Gitters \(\mathcal{L}(B)\) mit der
Basis \(B= \begin{pmatrix} 2 & -2 \\ 2 & 4 \end{pmatrix}\) durch die
roten Punkte dargestellt. Wie man sehen kann, stellt \(H=
\begin{pmatrix} 2 & 0 \\ -4 & 6 \end{pmatrix}\) ebenfalls eine Basis für
dasselbe Gitter dar. Hier gilt also \(\mathcal{L}(B)=\mathcal{L}(H)\).
Gitterprobleme
Es existieren verschiedene Arten von Gitterproblemen, darunter solche,
die sich effizient mithilfe von Algorithmen aus der linearen Algebra
lösen lassen. Beispiele hierfür sind:
- Sei \(\mathcal{L}\) ein Gitter. Bestimmung, ob für einen gegebenen
Vektor \(c\) gilt \(c \in \mathcal{L}\).
- Sei \(B\in \mathbb{R}^{n\times m}\) eine Basis, für das Gitter \(\mathcal{L}\). Bestimmung einer weiteren Basis \(H \neq B\) für \(\mathcal{L}\).
- Sei \(B\in \mathbb{R}^{n\times m}\) eine Basis, für das Gitter \(\mathcal{L}\). Bestimmung einer weiteren Basis \(H \neq B\) für \(\mathcal{L}\).
Zusätzlich gibt es Gitterprobleme, die als besonders schwer lösbar
gelten und sogar gegen Quantenalgorithmen resistent sein sollen. Aus
diesem Grund dienen diese Probleme als Grundlage für Verfahren in der
gitterbasierten Kryptografie. Im Folgenden werden diese kurz
vorgestellt.
Shortest Vector Problem (SVP)
Sei \(\mathcal{L}\) ein Gitter mit einer Basis \(B\in
\mathbb{R}^{n\times m}\), und \(\lambda(\mathcal{L})\) die Länge des
kürzesten Vektors in \(\mathcal{L}\), der nicht der Nullvektor ist. Nun
soll der Gitterpunkt gefunden werden, der dem Ursprung am nächsten
liegt. Gesucht wird also ein Vector \(r \in \mathcal{L}\), für den
\(||r||=\lambda(\mathcal{L})\) gilt.
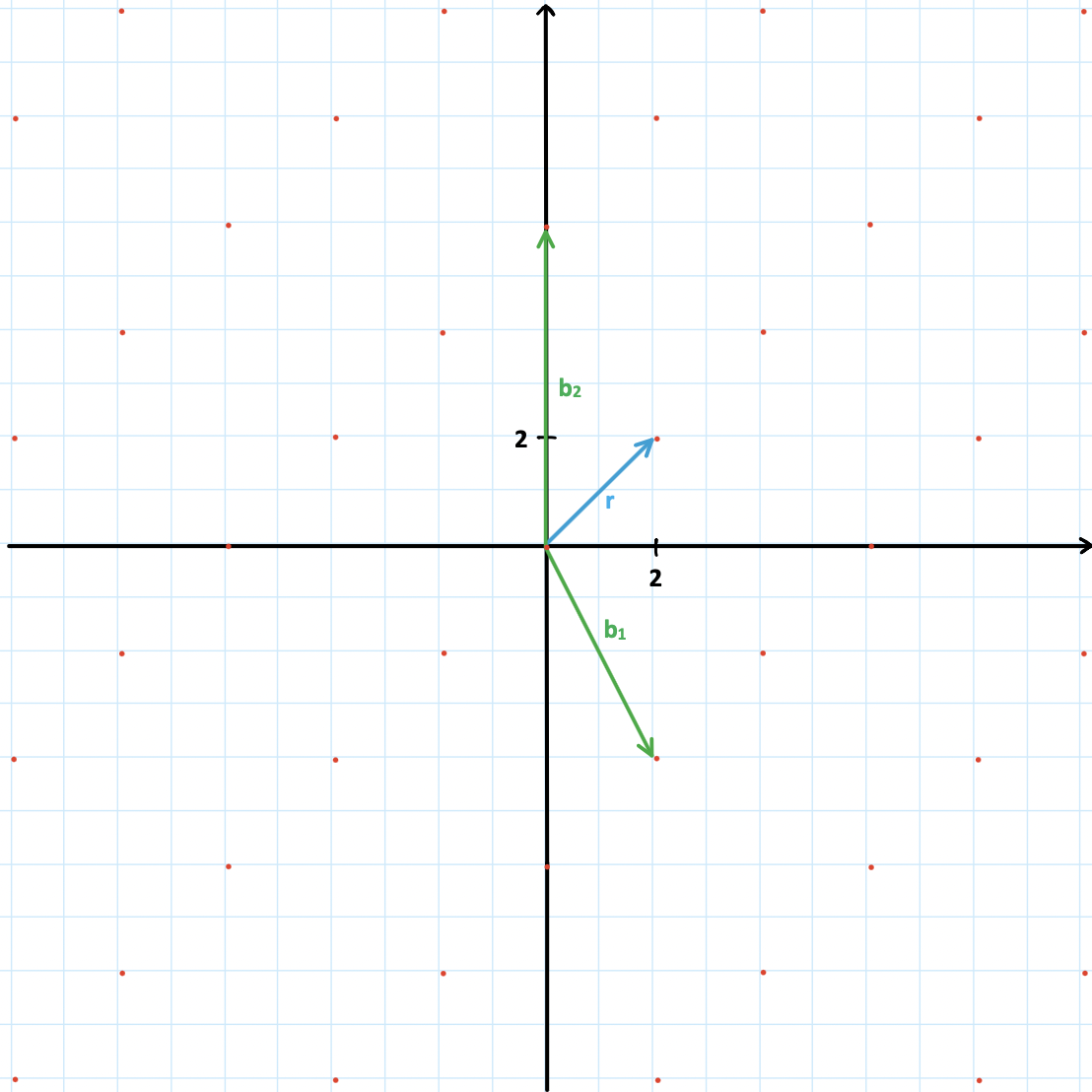
Abbildung 2: 2-dimensionales Gitter mit der Basis \(B=\{b_1,b_2\}\)
und dem kürzesten Vektor \(r\)
Closest Vector Problem (CVP)
Angenommen, \(\mathcal{L}\) ist ein Gitter mit einer Basis \(B\in
\mathbb{R}^{n\times m}\), und \(q \in \mathbb{R}^n\) ein Punkt außerhalb
des Gitters. Man sucht den Gitterpunkt, der \(q\) am nächsten liegt. Das
Ziel besteht also darin, einen Punkt \(p \in \mathcal{L}\) zu finden,
für den die Distanz \(||p-q||\) minimal ist.
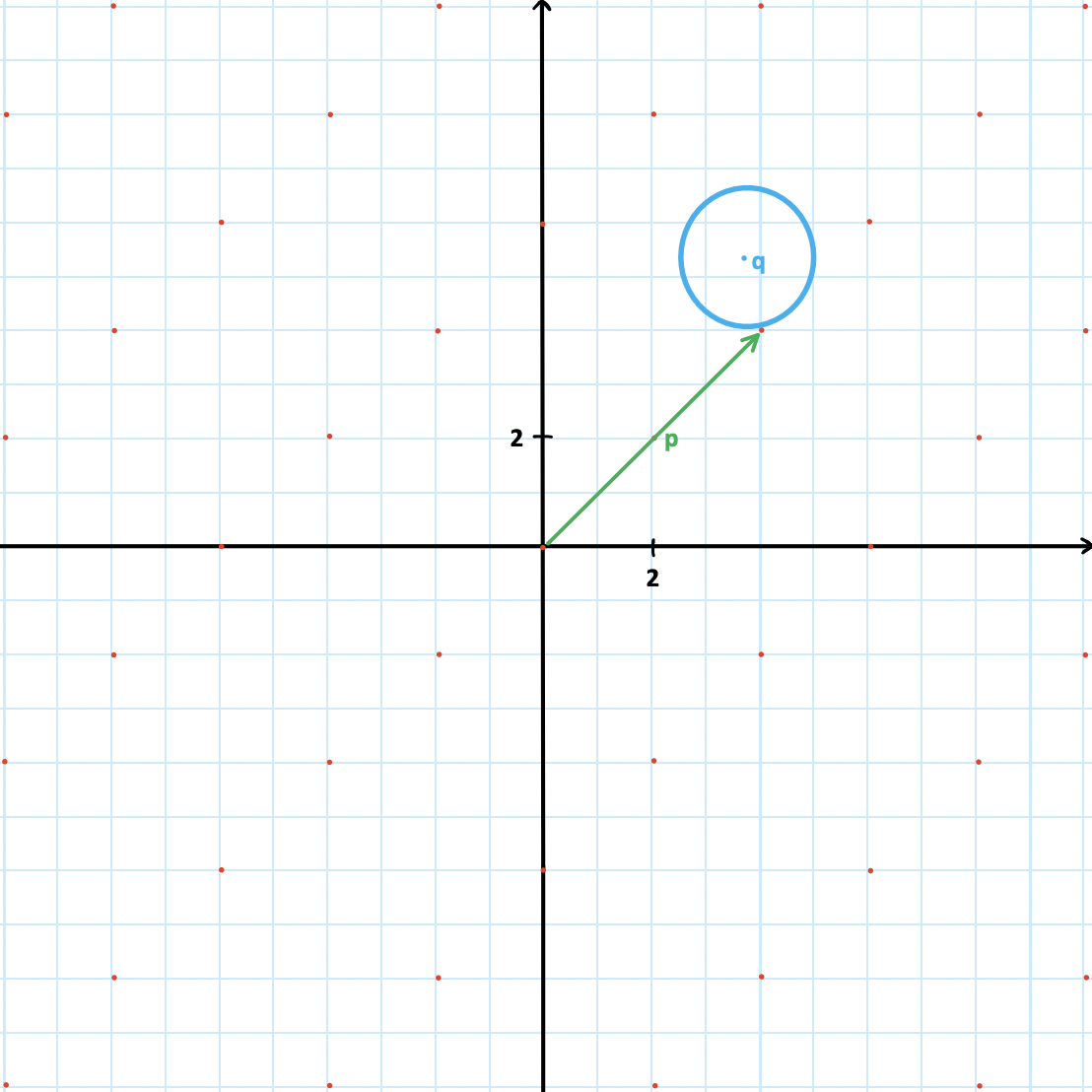
Abbildung 3: 2-dimensionales Gitter mit \(p\) als nahesten Vektor zu
\(q\)
GGH Kryptosystem
Das GGH-Kryptosystem, benannt nach seinen Entdeckern Oded Goldreich,
Shafi Goldwasser und Shai Halevi, wurde 1997 vorgestellt und basiert auf
der vermuteten Schwierigkeit des Closest Vector Problems. Obwohl das
GGH-Kryptosystem heutzutage nicht mehr als sicher gilt, dient es
aufgrund seiner einfachen Verständlichkeit als solider Ausgangspunkt, um
sich tiefer mit der gitterbasierten Kryptografie zu beschäftigen. Viele
seiner Elemente finden auch in aktuellen gitterbasierten Verfahren
Anwendung. Im Allgemeinen funktioniert das GGH-Kryptosystem wie folgt:
- Privater Schlüssel
Als privaten Schlüssel verwendet man eine wohlgeformte Basis \(B \in
\mathbb{R}^{n\times n}\) eines Gitters. Ein typischer Parameter ist
beispielsweise \(n = 300\). Unter einer wohlgeformten Basis versteht man
eine Basis, deren Spaltenvektoren möglichst kurz sind und nahezu
orthogonal zueinander stehen. Durch eine solche Basis kann man bestimmte
Varianten des Closest Vector Problems in \(\mathcal{L}(B)\) effizient
lösen.
- Öffentlicher Schlüssel
Als öffentlichen Schlüssel verwendet man eine nicht wohlgeformte Basis
\(H\) für dasselbe Gitter. Hierbei sind die enthaltenen Spaltenvektoren
möglichst lang und nahezu parallel zueinander ausgerichtet. Trotz dieser
Unterschiede muss \(\mathcal{L}(B)=\mathcal{L}(H)\) gelten.
Kryptoanalytisch betrachtet ist die sogenannte Hermite-Normalform (HNF)
von \(B\) die optimale Wahl. Dabei handelt es sich um eine ganzzahlige
Matrix in oberer oder unterer Dreiecksmatrixform, die beispielsweise
mithilfe des sogenannten Nemhauser/Wolsey-Algorithmus (s.
5.4.) aus \(B\)
abgeleitet werden kann und eine Basis für dasselbe Gitter wie \(B\)
darstellt. Die Hermite-Normalform ist eindeutig für jedes Gitter und
kann aus jeder beliebigen Basis des entsprechenden Gitters berechnet
werden. Anders ausgedrückt: Ein Angriff auf einen beliebigen
öffentlichen Schlüssel \(H\) ist stets höchstens so schwierig wie ein
Angriff auf die entsprechende Hermite-Normalform HNF\((H)\). Aus diesem
Grund verwendet man sie als öffentlichen Schlüssel.
Zusätzlich muss ein Parameter \(p \in \mathbb{N}\) festgelegt werden,
der den maximalen betragsmäßigen Wert der zufälligen Komponenten des
Fehlervektors \(e\) bei der Verschlüsselung repräsentiert. Dieser
Parameter muss so gewählt werden, dass für einen zufälligen Vektor \(e
\in [-p,p]^n\) der Ausdruck \(\lfloor B^{-1}e \rceil = 0\) sehr
wahrscheinlich und \(\lfloor H^{-1}e \rceil = 0\) sehr unwahrscheinlich
ist (\(\lfloor a \rceil\) bedeutet, dass die Komponenten von \(a\) auf
die nächste ganze Zahl gerundet werden sollen).
- Verschlüsselung
Um einen Klartext sicher zu verschlüsseln, wird er zunächst auf einen
Gitterpunkt \(m \in \mathcal{L}\) abgebildet. Dies geschieht, indem der
Klartext als ganzzahliger Spaltenvektor \(x \in \mathbb{Z}^n\)
betrachtet und mit der öffentlichen Basis \(Hx = m\) gebildet wird. Die
einzelnen Komponenten von \(x\) repräsentieren dabei die Koeffizienten
der Linearkombination mit den Spaltenvektoren von \(H\), die den
berechneten Gitterpunkt \(m\) ergeben. Anschließend wird diesem Punkt
ein zufälliger Fehler \(e \in [-p,p]^n\) mit ganzzahligen Komponenten
aufaddiert.
- Entschlüsselung
Um den Klartext \(x\) aus einem gegebenen Geheimtext \(c\)
wiederherzustellen, muss im ersten Schritt der Gitterpunkt \(m\)
bestimmt werden, der \(c\) am nächsten liegt. Dieser lässt sich mithilfe
der wohlgeformten Basis \(B\) und dem Rundungsverfahren von Babai wie
folgt berechnen:
\(m = B \lfloor B^{-1}c \rceil\)
Das ist möglich da:
\(B \lfloor B^{-1}c \rceil\ = B \lfloor B^{-1}(m+e) \rceil\)
Durch Ausmultiplizieren erhält man:
\(B \lfloor B^{-1}(m+e) \rceil = B(\lfloor B^{-1}m \rceil + \lfloor
B^{-1}e \rceil)\)
Da \(m \in \mathcal{L}\) und \(B\) ebenfalls eine Basis von
\(\mathcal{L}\) darstellt, entspricht \(B^{-1}m\) der ganzzahligen
Linearkombination von \(m\) mit den Spaltenvektoren von \(B\) und muss
daher nicht mehr gerundet werden:
\(B(\lfloor B^{-1}m \rceil + \lfloor B^{-1}e \rceil) = B(B^{-1}m +
\lfloor B^{-1}e \rceil)\)
Da wir sowohl von einem kleinen Fehler \(e\) als auch von kurzen
Spaltenvektoren in \(B\) ausgehen, nehmen wir an, dass \(\lfloor B^{-1}e
\rceil = 0\) gilt. Also ist:
\(B(B^{-1}m + \lfloor B^{-1}e \rceil) = B(B^{-1}m) = BB^{-1}m = Im = m\)
Zuletzt lässt sich der Klartext \(x\) durch Auflösen von \(Hx = m\)
wiederherzustellen.
GGH Kryptosystem Beispiel
Betrachtet wird das zweidimensionale Gitter \(\mathcal{L}\) mit der
wohlgeformten Basis \(B = \begin{pmatrix} 2 & -2 \\ 2 & 4
\end{pmatrix}\) als privater Schlüssel und der Basis \(H = \)HNF\((B) =
\begin{pmatrix} 2 & 0 \\ -4 & 6 \end{pmatrix}\) und dem Parameter
\(p=1\) als öffentliche Schlüssel. Der Klartext, der verschlüsselt
werden soll, ist \(x = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\). Man
bildet also zuerst \(x\) auf einen Gitterpunkt \(m\) ab:
\(Hx = \begin{pmatrix} 2 & 0 \\ -4 & 6 \end{pmatrix}\begin{pmatrix} 1 \\
2 \end{pmatrix} = \begin{pmatrix} 2 \\ 8 \end{pmatrix} = m\)
Nun generiert man einen zufälligen Fehler \(e\) und addiert diesen zu
\(m\):
\(m + e = \begin{pmatrix} 2 \\ 8 \end{pmatrix}+ \begin{pmatrix} 1 \\ -1
\end{pmatrix} = \begin{pmatrix} 3 \\ 7 \end{pmatrix}= c\)
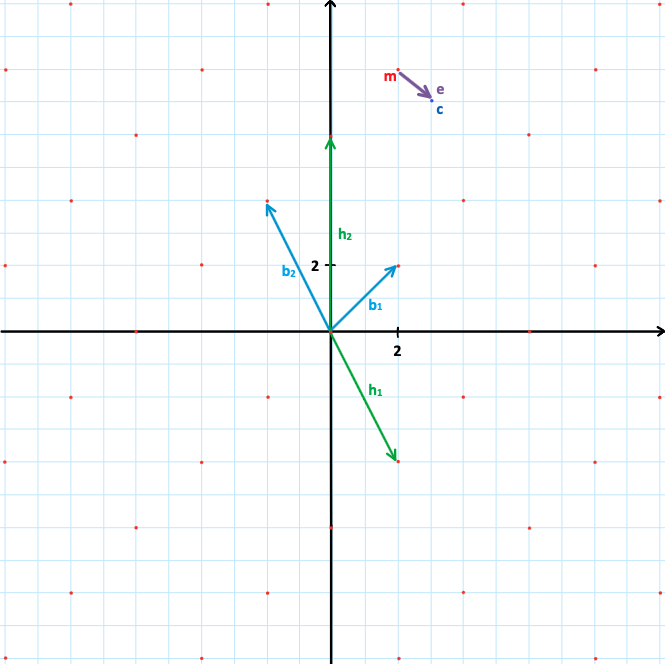
Abbildung 4: 2-dimensionales Gitter mit den Basen \(B=\{b_1,b_2\}\)
und \(H=\{h_1,h_2\}\), dem Gitterpunkt \(m\), dem Fehler \(e\) und dem
Geheimtext \(c\)
Jetzt kann der Empfänger den Klartext \(x\) mithilfe des privaten
Schlüssels \(B\) aus \(c\) wiederherstellen. Dafür rechnet man:
\(m = B \lfloor B^{-1}c \rceil = \begin{pmatrix} 2 & -2 \\ 2 & 4
\end{pmatrix} \Biggl\lfloor \begin{pmatrix} 2 & -2 \\ 2 & 4
\end{pmatrix}^{-1} \begin{pmatrix} 3 \\ 7 \end{pmatrix}\Biggl\rceil\)
\(= \begin{pmatrix} 2 & -2 \\ 2 & 4 \end{pmatrix} \Biggl\lfloor
\begin{pmatrix} \frac{1}{3} & \frac{1}{6} \\ -\frac{1}{6} & \frac{1}{6}
\end{pmatrix} \begin{pmatrix} 3 \\ 7 \end{pmatrix}\Biggl\rceil\)
\(= \begin{pmatrix} 2 & -2 \\ 2 & 4 \end{pmatrix} \Biggl\lfloor
\begin{pmatrix} \frac{13}{6} \\ \frac{2}{3} \end{pmatrix}\Biggl\rceil\)
\(= \begin{pmatrix} 2 & -2 \\ 2 & 4 \end{pmatrix} \begin{pmatrix} 2 \\ 1
\end{pmatrix} = \begin{pmatrix} 2 \\ 8 \end{pmatrix} = m\)
Der Empfänger kann also erfolgreich den Klartext wiederherstellen:
\(x = H^{-1}m = \begin{pmatrix} 2 & 0 \\ -4 & 6 \end{pmatrix}^{-1}
\begin{pmatrix} 2 \\ 8 \end{pmatrix} = \begin{pmatrix} \frac{1}{2} & 0
\\ \frac{1}{3} & \frac{1}{6} \end{pmatrix} \begin{pmatrix} 2 \\ 8
\end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\)
Sollte ein Angreifer versuchen, den Klartext mittels \(H\)
wiederherzustellen, erhält dieser:
\(m_H = H \lfloor H^{-1}c \rceil = \begin{pmatrix} 4 \\ 4
\end{pmatrix}\)
bzw.
\(x_H = H^{-1}m_H = \begin{pmatrix} 2 \\ 2 \end{pmatrix}\)
was nicht korrekt ist.