Willkommen auf PQKdemo.de
Diese Webseite widmet sich der Vermittlung der Grundlagen der
Post-Quanten-Kryptografie. Ziel ist es, nicht nur theoretische Konzepte
zu vermitteln, sondern auch praktische Einblicke durch die Demonstration
der besprochenen Inhalte zu bieten. Die Inhalte richten sich an
Interessierte mit einem Grundverständnis für mathematische Konzepte aus
den Bereichen der linearen Algebra und modularen Arithmetik.
Im Folgenden werden aus Gründen der Lesbarkeit und ohne Exklusion
Begriffe wie 'Sender', 'Empfänger' und 'Angreifer' im generischen
Maskulinum verwendet. Jedoch schließt dies explizit Personen jeglichen
Geschlechts ein.
Was ist Kryptografie?
Die Kryptografie ist eine Wissenschaft, bei der man sich mit der
Verschlüsselung von Informationen befasst. Hierbei werden Verfahren
entwickelt, um aus einer Nachricht (dem Klartext) einen nicht mehr
lesbaren Geheimtext zu generieren. Dieser Geheimtext wird an einen
Empfänger übertragen. Allein dieser Empfänger sollte dazu in der Lage
sein, den Klartext aus dem Geheimtext wiederherzustellen. Daher ist es
möglich, den Geheimtext bedenkenlos über unsichere Kanäle, wie das
Internet, zu übermitteln, wo die Nachricht möglicherweise von Dritten
abgefangen wird.
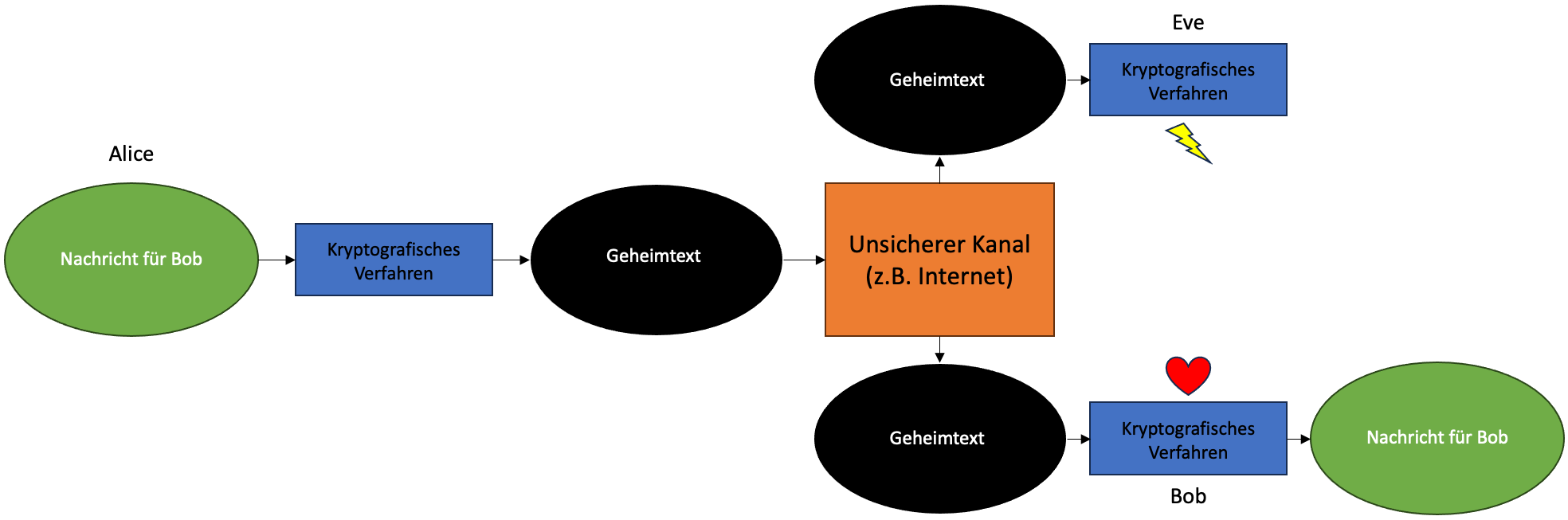
Abbildung 1: Visuelle Darstellung einer verschlüsselten Kommunikation
Tatsächlich geht es in der modernen Kryptografie aber nicht nur um die
Verschlüsselung von Klartexten, sondern darüber hinaus um das Thema
Informationssicherheit im Allgemeinen. Dabei gilt es, die folgenden
Schutzziele zu gewährleisten:
- Vertraulichkeit: Der Inhalt einer Nachricht soll ausschließlich berechtigten Personen offengelegt werden können (siehe Abbildung 1).
- Integrität: Es wird gewährleistet, dass der Inhalt einer Nachricht den Empfänger vollständig und unverändert erreicht.
- Authentizität: Gewährleistung, dass die Identität eines jeden Kommunikationspartners verifiziert werden kann. Das bedeutet, sicherzustellen, dass es sich bei einem Kommunikationspartner tatsächlich um diejenige Person handelt, die sie vorgibt zu sein.
- Nichtabstreitbarkeit: Es soll verhindert werden, dass der Sender einer Nachricht die Urheberschaft der Nachricht leugnen kann.
Heutzutage sind eine Vielzahl erprobte Konzepte bekannt, die es
ermöglichen, Informationssysteme zu konstruieren, in denen die oben
genannten Schutzziele sichergestellt sind. Aufgrund dieser Konzepte ist
die digitale Kommunikation, wie man sie heute kennt, erst möglich.
Die Sicherheit moderner Informationssysteme beruht heutzutage auf
Verfahren, die auf der vermuteten Schwierigkeit bestimmter
mathematischer Probleme basieren. Um beispielsweise einen Geheimtext zu
entschlüsseln, muss dieses spezifische Problem gelöst werden. Dem
rechtmäßigen Empfänger ist ein Geheimnis bekannt, mit dem er dazu in der
Lage ist. Ohne Kenntnis dieses Geheimnisses ist es einem Angreifer aber
nicht möglich, das Problem effizient zu lösen.
Ein Beispiel hierfür ist die Faktorisierung einer sehr großen
natürlichen Zahl. Wenn man zwei 500-stellige Primzahlen miteinander
multipliziert, erhält man eine 1000-stellige Zahl. Es ist kein
klassischer Algorithmus bekannt, der diese 1000-stellige Zahl in kurzer
Zeit auf die beiden Primzahlen zurückführen kann. Sollte jedoch bereits
eine dieser beiden Primzahlen bekannt sein, kann die zweite durch
einfaches Dividieren in kürzester Zeit berechnet werden.
Warum Post-Quanten-Kryptografie?
In nicht allzu ferner Zukunft ist zu erwarten, dass eine neue Art von
Computern verfügbar sein wird, die heute nur in Forschungseinrichtungen
existiert: die Quantencomputer. Diese stellen leistungsstarke Werkzeuge
dar, mit denen Berechnungen effizient durchgeführt werden können, die
mit herkömmlichen Computern mehrere Jahre dauern würden oder sogar
gänzlich unmöglich wären. Quantenalgorithmen wie beispielsweise der
Grover-Algorithmus oder der Algorithmus von Shor können damit ausgeführt
werden.
Der Grover-Algorithmus ist ein Quantenalgorithmus, der einen
quadratischen Speedup auf Suchprobleme ermöglicht. Ein
Brute-Force-Angriff, also das Ausprobieren aller möglichen Lösungen, der
\(2^{128}\) Schritte auf einem herkömmlichen Computer benötigt, kann auf
einem Quantencomputer in \(\sqrt{2^{128}} = 2^{64}\) Schritten
ausgeführt werden. Durch Verdoppeln des Sicherheitsparameters von
\(128\) auf \(256\) kann dem entgegengewirkt werden. Daher stellt der
Grover-Algorithmus keine große Herausforderung im Kontext der
Kryptografie dar.
Der Algorithmus von Shor hingegen stellt die Kryptografie vor eine große
Herausforderung: Mit dem Shor-Algorithmus lassen sich mathematische
Probleme wie das Faktorisierungsproblem oder das Problem des diskreten
Logarithmus in Polynomialzeit lösen. Diese beiden Probleme bilden das
Fundament für die Sicherheit vieler verbreiteter Kryptografieverfahren.
Dementsprechend können die betroffenen Verfahren nicht mehr als sicher
deklariert werden und müssen ersetzt werden.
Deshalb wird an Verfahren der Post-Quanten-Kryptografie geforscht.
Diesen Verfahren liegen andere mathematische Problemstellungen zugrunde,
von denen vermutet wird, dass sie nicht einmal mit Quantencomputern
effizient gelöst werden können. Damit stellen diese Verfahren die
Kandidaten dar, die zukünftig die durch die Quantencomputer entstehenden
Sicherheitslücken füllen werden. Die Verfahren der
Post-Quanten-Kryptografie lassen sich in verschiedene Verfahrensfamilien
unterteilen. Die fünf prominentesten sind:
- Multivariate Kryptografie
- Hashbasierte Kryptografie
- Gitterbasierte Kryptografie
- Codebasierte Kryptografie
- Isogeniebasierte Kryptografie
Jede dieser Verfahrensfamilien bietet eigene Anwendungsgebiete und
spezifische Vor- und Nachteile. Im Folgenden wird die Möglichkeit
geboten, drei dieser fünf Familien kennenzulernen. Dabei werden
Grundlagen erläutert und jeweils ein elementares Verfahren vorgestellt
und demonstriert. Zu jedem vorgestellten Verfahren ist ein
Online-Rechner integriert, mit dem Berechnungen mit eigenen Parametern
und Werten durchgeführt werden können. Darüber hinaus erhält man
Einsicht in den Programmcode, der bei den entsprechenden Berechnungen
ausgeführt wird.
Aufrufe dieser Webseite: 11416